平方根で出てくる根号√(ルート)が、なぜこのような形になったのかを紹介します。 Ⅰ 平方根の必要性 中学3年生の教科書にも載っている平方根の定義は次の通りです。 2乗して 秘書ザピエル今回は、「平方根(へいほうこん)」についての内容です第4回として、「平方根の求め方 分数 小数 実践編」について、解説してもらいたいと思います。では先生、お願いします!数学おじさん したがって、36の平方根は6と6の2つがある のです。(それぞれ正の平方根、負の平方根と言います) つまり、 ある数の平方根はプラスとマイナスの2種類ある ということを覚えておきましょう! テストでは正と負、両方書かないとバツになりますよ!

平方根はこれで完璧 平方根の定義からルートの計算 近似値の問題の解き方まで
平方根 足し算 なぜ
平方根 足し算 なぜ-平方根は、ポアソンに対してほぼ分散安定化されます。 平方根には、 3 を追加するなど、プロパティを改善するさまざまなバリエーションがあります 3 8 3 8 平方根を取る前に、またはFreemanTukey( バツ − − √ X 1 − − − − − √ X X 1 ただし、平均値も調整されることがよくありまルートの足し算は、√の中の数が重要です。 ルートの中の数が同じ場合、違う場合で下記のように計算が変わります。 ルートの中の数が同じ場合 ⇒ √5√5=2√5のように簡単にできる。 ルートの中の数が違う場合 ⇒ √5√3=√5√3のまま。 これ以上簡単な形にできない。 ルートは平方根を表す記号で根号(こんごう)といいます。 √aは2乗してaになる数を




あさお ちょっといい話 3月14日は 数学の日 円周率の近似値3 14に因んで 数学 と 算数 の違い 算数は 日常生活で必要となる足し算等の計算で正確な答を出す事が目的で 計算力を高めるための学問 数学は 平方根等日常生活では目にしない抽象的
開平法の原理 与えられた正の数の正の平方根の小数表示を求めるために、ここではまず漸化式を立てて、一般的な求値法を求める。 そして、求値の明確化のために、開平法と呼ばれる筆算の原理を導出する。 以下は十進法表示の場合だが、他の位取り記数法でも同様な計算で求められる。平方根とは 2 乗すると a になる数のことを a の平方根といいます。つまり、式 x 2 = a の x に当てはまる数が a の平方根です。1 つの正の数に対して、その平方根は正と負の 2 つあります。 平方根は、二乗根や自乗根と言われることもあります。 平方根の計算 単元 平方根, 「平方根の基礎です。 平方根の原理を理解するのにお使いください。できる限り短くまとめました。 得意な方、応用をやりたいという方には向いていません。 有理化や、ルートの数を簡単にする方法は書いていません。 」, 学年 中学3年生, キーワード 平方根,ルート,中3,数
開平法とは,与えられた正の有理数の平方根の値を筆算を用いて求める手続き(アルゴリズム)のことです. たとえば, $$\sqrt{2}=$$ $$\sqrt{3}=$$ などの近似式をご存知の方は多いと思いますが,開平法を用いれば,どのような有理数の平方根の近似値も筆算だけで求めることができます.平方根では掛け算と割り算を学びます。 一般的に数学では、最初に足し算と引き算を学びます。 ただ平方根については、掛け算と割り算のほうが簡単です。 根号(ルート)の数字をそのまま掛け算すればいいからです。 ただ、平方根の掛け算にはルールがあります。 また、なぜルート同士の掛け算をしてもいいのか理解している人は少ないです。 平方根の「平方根」というのは2つあります。 たとえば、 ・9の平方根は? と聞かれた場合、 ・2乗すると9になる数は? という意味なので、 「+3と、-3」 の 2つの答えがあります。 (ここまではもう大丈夫ですね!) 同じことを根号(ルート)で表せば、
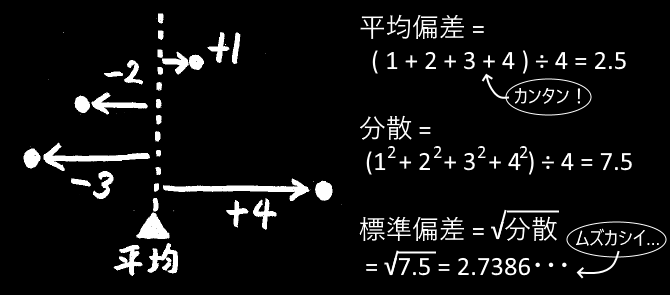
・なぜ、差の2乗を計算するのか? ・差そのものであってはいけないのか? ・なぜ、分散と標準偏差の2種類があるのか? 最後の疑問については「分散が2乗した結果なので、元の単位に戻すために平方根をとる必要がある」のだと説明されます。 でもじつは、平方根の計算でめんどいのは、 ルートの足し算・引き算 なんだ。 足し算・引き算をマスターすれば大丈夫。 どんな平方根の計算もクリアできるはずさ。 今日はその、 平方根(ルート)の足し算・引き算の計算方法 を解説していくよ。平方根は「 ボールを投げたときの放物線運動 (二次方程式の解の公式)」や「 株価の変動リスク の評価(標準偏差)」など、色んな分野の計算法が見えてくるので、理解できる世界がグッと広がってくる単元です。 ぼく自身、複雑にみえていた色んな数式を自分でも解けるようになって




平方根 ルート の足し算 引き算の仕方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



平方根 ルート の計算方法まとめ おさえておくべき4つのポイント アタリマエ
Account ログイン ユーザー登録 なぜ素数の平方根までチェックして、それが素数かどうかを判断するのですか? 392 数が素数かどうかをテストするために、なぜその数の平方根までしか割り切れ平方根の足し算とかけ算とわり算の違いを教えてください💦 中学生 数学 平方根の問題↓で (2√53)(4√5) 模範解答が、2211√5で私の解答が11√522になったのですが、これでは間違えになりますか?平方根計算機 オンラインの平方根計算機を使用して、入力した数値の平方根を見つけます。 平方根 数学では、数値xの平方根は、r 2 = xとなるような数値rです。 例えば、 1 5 2 = 25であるため、25の平方根は5です。 3 2の平方根はおよそです。 3 Piの平方根(π)は約です




平方根の足し算と引き算 ルート計算のやり方や分数の求め方 リョースケ大学




平方根 ルート の重要な計算方法まとめ 数学fun
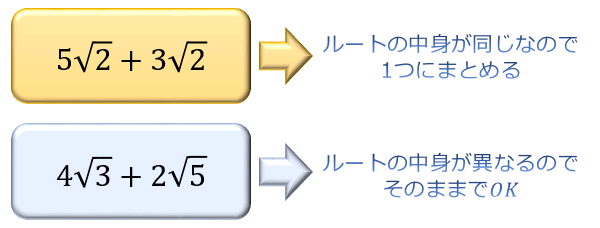
平方根の足し算と引き算は、 ルートの中身が同じ数を1つにまとめます。 パッと見は中身が異なる場合でも、 ルートの中身を簡単にすると同じになるケースもある ので、ルートの中身を可能な限り簡単にしてから足し算・引き算を行います。 50 18 を計算 平方根のルートの中の値が違う数同士は何故計算出来ないのでしょうか? 何方算数的に解説して下さい。 まず、質問を整理しましょう。>平方根のルートの中の値が違う数同士は何故計算出来ないのでしょうか?これは、下記の質問に書き直せます。 質問x,y,zが整数とする。なぜ、√x√y=√zが(1) 、なぜ平方根までの数でよいのか 32 なら、 1,2,4,8,16,32 といった具合に、数には約数があり、約数には、掛け合わせると、元の数になる、つまり、対になる数がありこの数が折り返しているのが平方根なのである。 (2) 、なぜ素数だけでよいのか




なぜ ルート 平方根 の中身を足し算 引き算しちゃいけないの Qikeru 学びを楽しくわかりやすく



超基本だけど入試にも出る 平方根の基礎問題 2日目 ベントー
中学3年生向け!平方根はこうやって解く!平方根を基本から徹底解説!④ 21年2月1日 学習内容解説ブログサービスリニューアル・受験情報サイト開設のお知らせ 学習内容解説ブログをご利用下さりありがとうございます。 開設以来、多くの皆様にご利用いただいております本ブログ 計算しましょう。 √2 2 √5√2 2 2 5 2 後ろの分数の分母を有理化して計算すればなんてことはないですね。 まずは有理化してから計算してみましょう。 √2 2 √5√2 2 2 5 2 = √2 2(√5−√2) (√5√2)(√5−√2) = 2 2 ( 5 − 2) ( 5 2) ( 5 − 2) = √2 2(√5−√2) 3 = 2 2 ( 5 − 2) 3 = 3√2 3 2(√5−√2) 3 = 3 2 3 2 ( 5 − 2) 3 = 3√22√5−2√2 3 = 3 2 2 5 − 2 2 3平方根のかけ算、割り算は、根号の中どうし、外どうし計算する。 30=6×5なので 6 × = 6 5 98=7 2 ×2, 27=3 3 なので 98 = 7 2 27 = 3 3 よって 98 × 27 = 7 2 ×3 3 = 7×3× 2×3 =21 6 6 10 ÷3 2 = 6 3 10 2 = 2 5 平方根の足し算、引き算はルートの中が全く同じときだけ、「同類項をまとめる」ように計算できる。 また



なぜ分散は2乗の和なのか 小人さんの妄想




なぜ 1 は掛け算で 2 は足し算なのですか Clear
平方根の足し算、引き算についてサクッと解説してきたけど理解してもらえたかな? 掛け算や割り算とはちょっと計算ルールが異なるので注意が必要だね。 ルートの中身は足しちゃダメ!ってことを肝に銘じておこう。 ゆい OK,OK~♪ 理解しましたぜ! 同じルートどうしを足したり、 なぜ偏差平方和を求めるの? さぁ先ほどの偏差を平均化してみましょう! そうすることで、偏差の代表値が出せるハズ・・・ あれ?0になった。今回は標準偏差は0なのか? いえ、そうではありません。実は偏差は平均化する事が出来ないのです。 これは、式で読み解くと納得しやすいです 35は元の式\(\sqrt{5} \times \sqrt{7}\)を2乗したものなので、35の平方根 1 2乗してある数になる数をある数の平方根と言います。 が、\(\sqrt{5} \times \sqrt{7}\)の平方根と言うことになり




なぜ ルート 平方根 の中身を足し算 引き算しちゃいけないの Qikeru 学びを楽しくわかりやすく
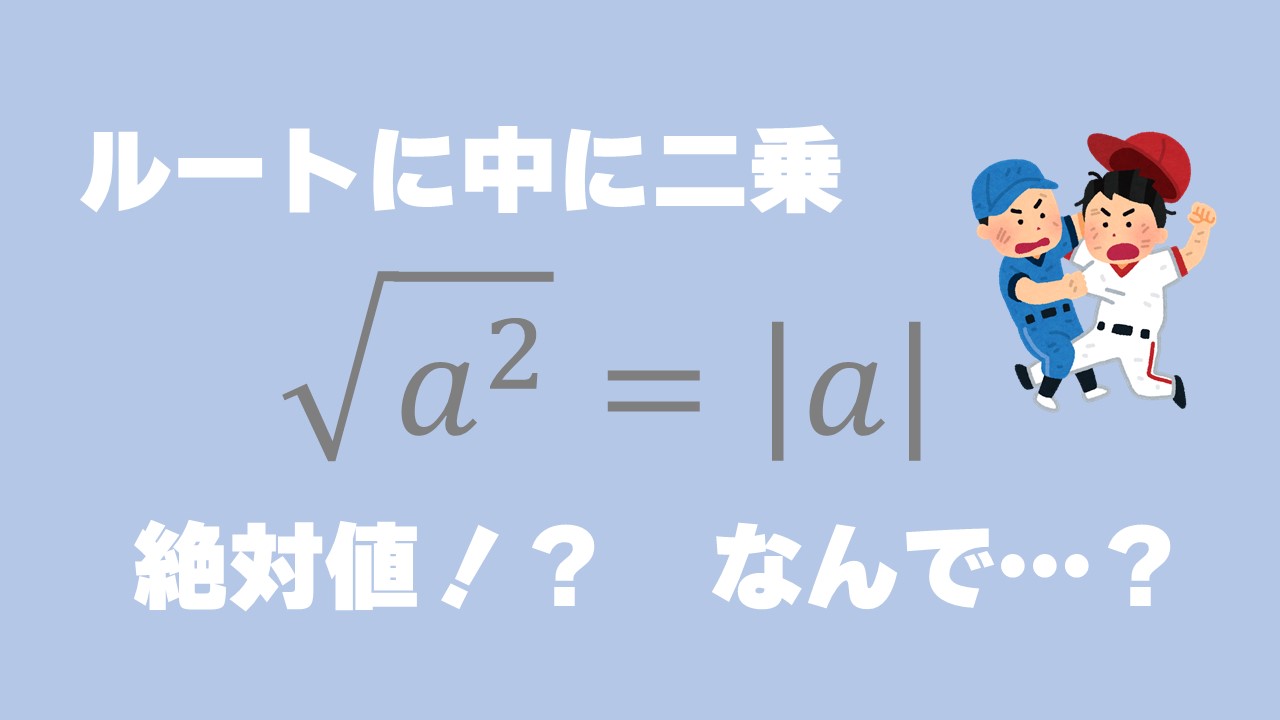



ルートの中身が絶対値に なんで場合分けが必要なのか 数スタ
平方根の解が2つなら、立方根の解は3つの方が美しいと思いませんか? 質問者は恐らく数概念の拡張の話をご存知無いと思います。(知らなければググってください。) 昔々、数といえば自然数しかなかった時代。 数は数えるだけだった時代。一般に、正方行列 a に対して、 x 2 =a を満たす正方行列 x を a の平方根行列と呼び 、記号で √ a あるいは a 1 ⁄ 2 と表す。平方根行列は存在するとは限らず、存在しても1つだけの場合や複数個の場合、無限個存在する場合がある。 平方根はなぜ必要? 平方根はなぜ必要なのでしょうか。 実生活では必要ないという方もいると思いますが、どうしたら平方根が生まれるのかなぁということについて考えてみます。 平方根は2乗してある数になる数のことを言います。



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス




平方根の足し算と引き算 ルート計算のやり方や分数の求め方 リョースケ大学
#23 平方根 − 68 − 高校講座・学習メモ √ のたし算とひき算 ここで、 27+ 12=? は、どうでしょう ですから、 27+ 12=3 3+2 3 ここで 3=aと平方根の計算で素因数分解が重要なのは、ルート内の数字を最小にできるからです。 その結果、足し算・引き算が可能になります。 リョースケ大学 平方根の掛け算・割り算:ルート計算と素因数分解のやり方 https//jtraditioncom/jp/root2html 平方根では掛け算と割り算を学びます。 一般的に数学では、最初に足し算と引き算を学びます。 ただ平方根についてはでもなぜ√の足し算は文字式に置き換えて考えなくてはならないのでしょう。 足し算なのにルートの中が4倍になるのがどうしても納得いきません。 どなたかわかりやすく説明していただけるとありがたいです。 よろしくお願いします。




ある問題を解いてみて 最終的に答えはゼロになるらしいのですが 何故 5にならないのか Clear




平方根 ルート の重要な計算方法まとめ 数学fun
平方根(ルート) 平方根の利用正方形の対角線、丸太、自然数を求める解き方は? いろんな利用問題を解説! kaztaro 中学数学・理科の学習まとめサイト! 平方根(ルート) ★有理化の仕方★やり方をまとめておくよ! 中学生 kaztaro
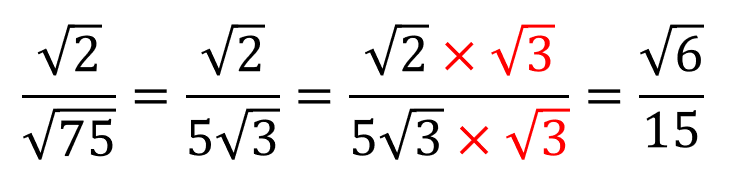



平方根 ルート の重要な計算方法まとめ 数学fun




あさお ちょっといい話 3月14日は 数学の日 円周率の近似値3 14に因んで 数学 と 算数 の違い 算数は 日常生活で必要となる足し算等の計算で正確な答を出す事が目的で 計算力を高めるための学問 数学は 平方根等日常生活では目にしない抽象的




平方根 ルート の足し算 引き算の仕方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




ルートの掛け算の計算はなぜ中の数字同士を計算することができるの さびねこ中学校




ルートの計算で分数の分母を有理化しないといけない理由とは さびねこ中学校




平方根 ルート の重要な計算方法まとめ 数学fun



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス



なぜ ルート 平方根 の中身を足し算 引き算しちゃいけないの Qikeru 学びを楽しくわかりやすく




平方根の計算 ルートを簡単にする方法がわかる3つのステップ Qikeru 学びを楽しくわかりやすく 21 平方根 計算 学び




平方根 ルート の重要な計算方法まとめ 数学fun




なぜ ルート 平方根 の中身を足し算 引き算しちゃいけないの Qikeru 学びを楽しくわかりやすく




なぜ ルート 平方根 の中身を足し算 引き算しちゃいけないの Qikeru 学びを楽しくわかりやすく
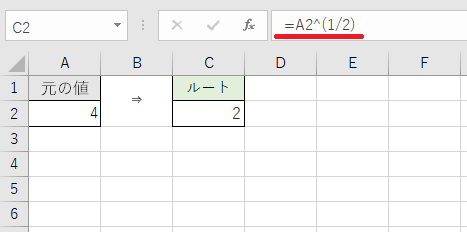



画像あり エクセルの関数を使ってルート 平方根 を計算 表示するには 基本と応用 ワカルニ




平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ




最も人気のある ルート の 計算 足し算 壁紙 配布




平方根 ルート の重要な計算方法まとめ 数学fun




素因数分解について 162を素因数分解したら9 2になるそうですが画像の 数学 教えて Goo
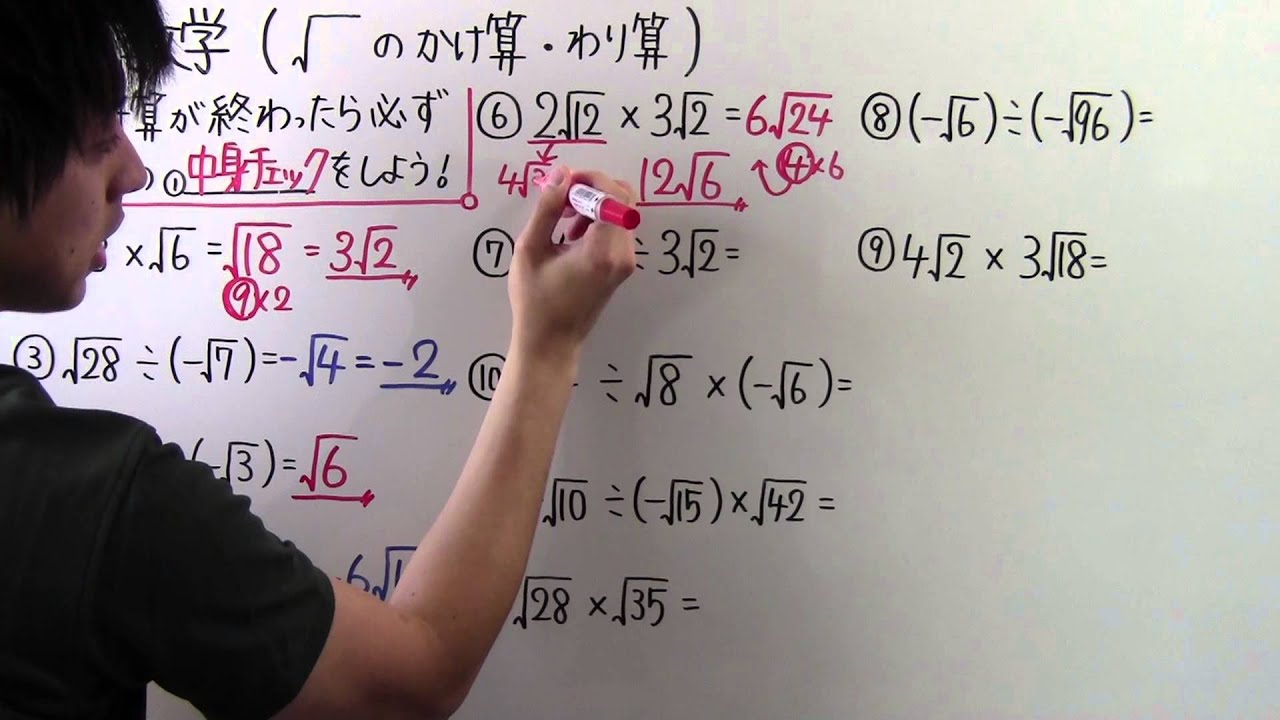



数学 中3 18 ルートのかけ算 わり算 Youtube




平方根 ルート の重要な計算方法まとめ 数学fun




楽天市場 増補改訂版 中学校3年分の数学が教えられるほどよくわかる ベレ出版 英語伝 Eigoden




人気の 平方根 動画 35本 ニコニコ動画



Wbuuyeznuk8inm
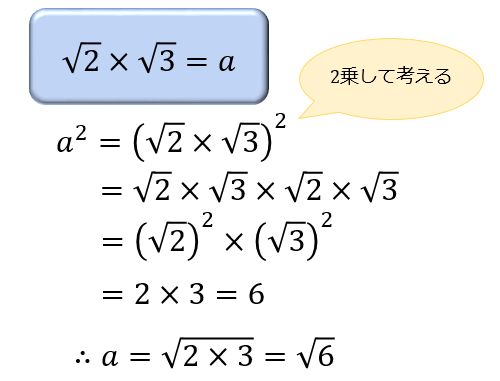



平方根 ルート の計算方法まとめ おさえておくべき4つのポイント アタリマエ




なぜ ルート 平方根 の中身を足し算 引き算しちゃいけないの Qikeru 学びを楽しくわかりやすく
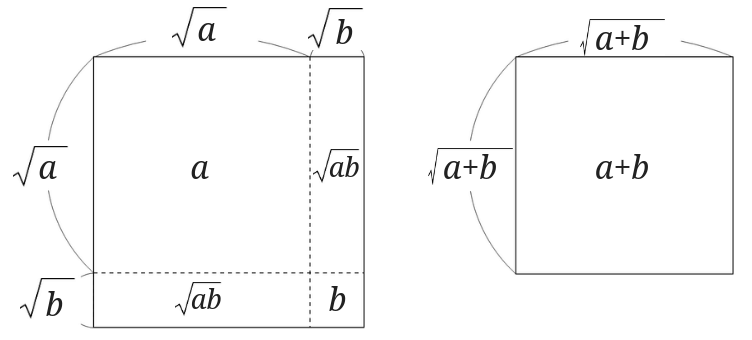



ルートの中が違う足し算や引き算の計算の仕方は 平方根の加減法をマスターしよう さびねこ中学校



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス




無理数の足し算が真値で出来る コンピュータより正確な計算機 発想力教育研究所 素数誕生のメカニズム



ルートの中が足し算の時とかけ算の時の ルートの外し方の違いを教 Yahoo 知恵袋




平方根の足し算と引き算 ルート計算のやり方や分数の求め方 リョースケ大学
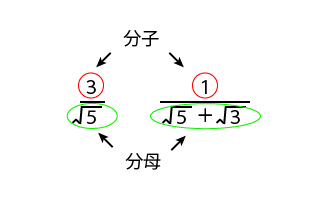



有理化 もう一度やり直しの算数 数学




なぜ ルート 平方根 の中身を足し算 引き算しちゃいけないの Qikeru 学びを楽しくわかりやすく




平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ




数学50点以下の受験生がすぐに点アップする10個の解法 平方根 中学数学ぐんぐんブログ



二重根号の外し方 解き方を丁寧に解説 マイナスの入ったパターンも攻略 Studyplus スタディプラス




Xの二乗 7の二乗 9の二乗 Xの二乗 32 とありますがなぜ引き算をするんですか Clear




平方根




数学 中3 21 ルートの計算のまとめ Youtube



数学の問題でlogの計算をしているんですけど なぜ写真のように Yahoo 知恵袋




平方根 ルート の重要な計算方法まとめ 数学fun



Q Tbn And9gctp9zr6n Jalfrwhljnb P6wu 5aij5qmymt9dfxspepxwxxtfm Usqp Cau



何故ルートの中同士で足し算をすることが出来ないのでしょうか Yahoo 知恵袋
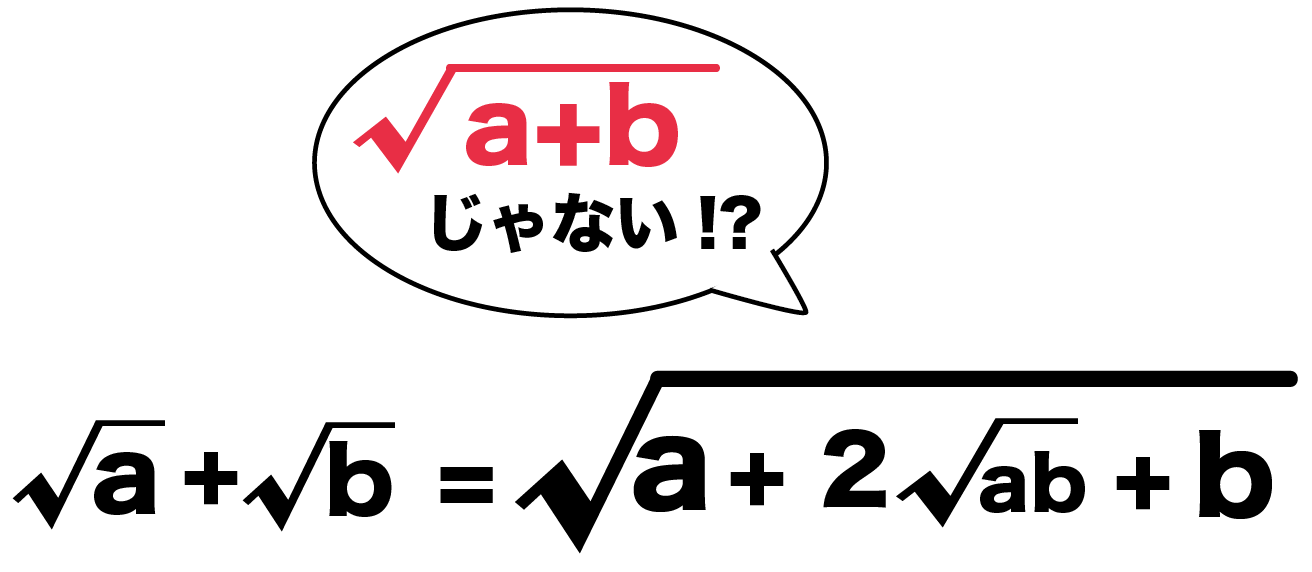



なぜ ルート 平方根 の中身を足し算 引き算しちゃいけないの Qikeru 学びを楽しくわかりやすく



3



なぜ ルート 平方根 の中身を足し算 引き算しちゃいけないの Qikeru 学びを楽しくわかりやすく



1




なぜこの部分がこのように変換されるのか教えてください Clear



2




平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ




中3数学 ルート 平方根 の計算方法における3つのコツ Qikeru 学びを楽しくわかりやすく



何故ルートの中同士で足し算をすることが出来ないのでしょうか Yahoo 知恵袋
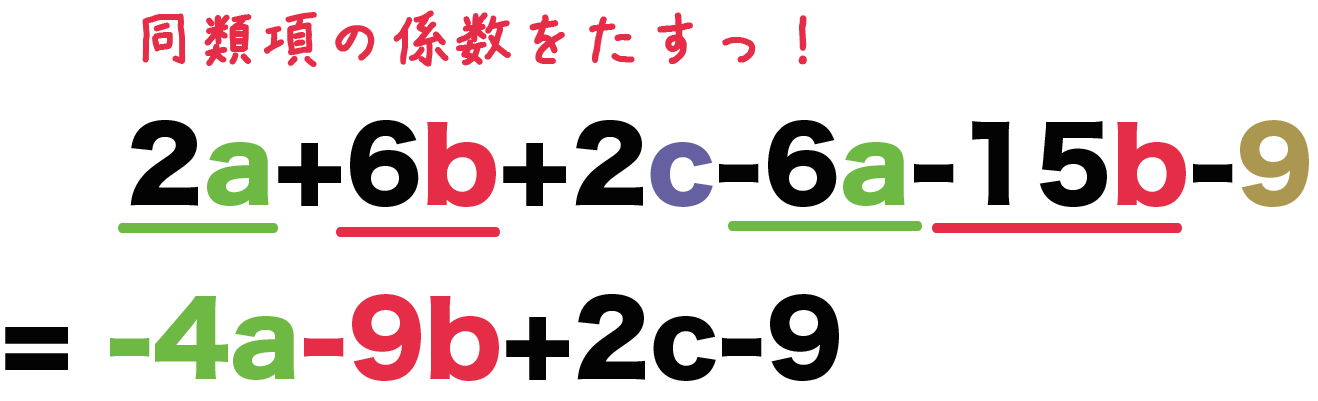



なぜ ルート 平方根 の中身を足し算 引き算しちゃいけないの Qikeru 学びを楽しくわかりやすく




愛されし者 ルート 計算 足し算




平方根 ルート の重要な計算方法まとめ 数学fun



高校入試の平方根をたった3分で 得意 にする方法 高校入試徹底対策ガイド




平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ




平方根 ルート の重要な計算方法まとめ 数学fun




なぜ ルート 平方根 の中身を足し算 引き算しちゃいけないの Qikeru 学びを楽しくわかりやすく




平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス




平方根 ルート の重要な計算方法まとめ 数学fun




平方根 ルート の足し算 引き算の仕方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




平方根はこれで完璧 平方根の定義からルートの計算 近似値の問題の解き方まで




なぜ ルート 平方根 の中身を足し算 引き算しちゃいけないの Qikeru 学びを楽しくわかりやすく




ルートの掛け算の計算はなぜ中の数字同士を計算することができるの さびねこ中学校




平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ




平方根 ルート の重要な計算方法まとめ 数学fun




平方根 ルート の足し算 引き算の仕方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




この式をaについて解くとき 2 Bを両辺にかけて解くのはなぜ間違いなのですか Clear



内の数字が異なる平方根の足し算 引き算について 中学三年生の者です 宿 Yahoo 知恵袋




なぜ ルート 平方根 の中身を足し算 引き算しちゃいけないの Qikeru 学びを楽しくわかりやすく




平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス




平方根 ルート の足し算 引き算の仕方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ



1



ルートの中が足し算の時とかけ算の時の ルートの外し方の違いを教 Yahoo 知恵袋




平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ



中学数学 平方根 1 について A二乗 Aの法則で が取れるのは Yahoo 知恵袋




至急 平方根の中の二乗について至急お願いします なんで2行目の式 数学 教えて Goo




中学3年生向け 平方根はこうやって解く 平方根を基本から徹底解説 学習内容解説ブログ




ルートの中が違う足し算や引き算の計算の仕方は 平方根の加減法をマスターしよう さびねこ中学校




分数の分子に足し算がある場合 約分が出来ないのはなぜですか 分子 数学 教えて Goo



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス
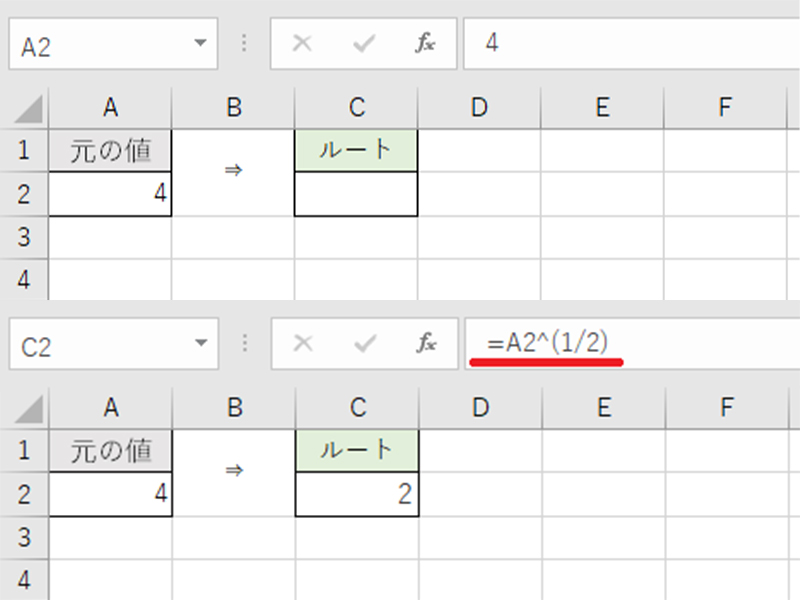



画像あり エクセルの関数を使ってルート 平方根 を計算 表示するには 基本と応用 ワカルニ




平方根の足し算と引き算 ルート計算のやり方や分数の求め方 リョースケ大学




平方根 ルート の足し算と引き算のやり方と計算問題 中学3年生数学 Irohabook




平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ




分母の有理化 分数の平方根で分母のルートを消すやり方 リョースケ大学



平方根 分数引き算 なぜ2 2 21になるのですか 0ではないので Yahoo 知恵袋




平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ




分母の有理化 分数の平方根で分母のルートを消すやり方 リョースケ大学



0 件のコメント:
コメントを投稿