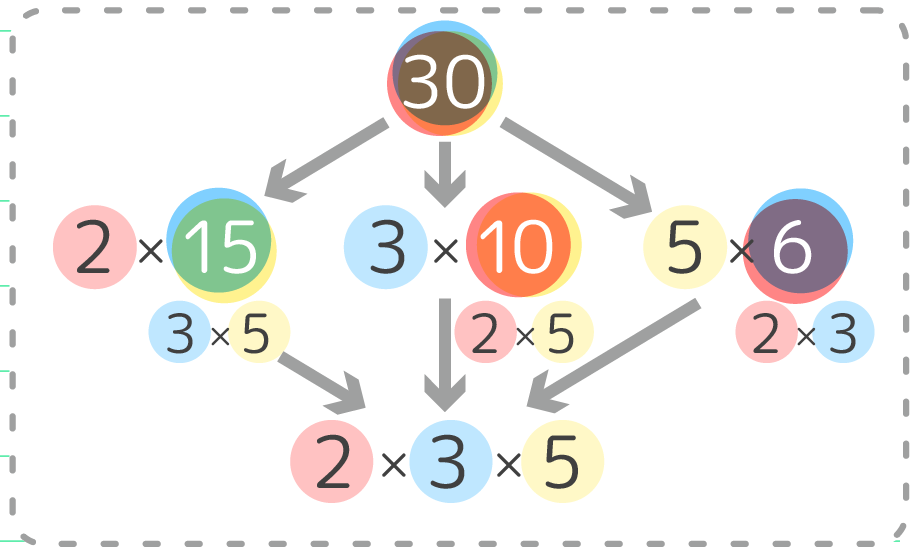
約数の(数)の求め方:素因数分解 約数の数・個数を求める場合は「素因数分解」が便利です。 素因数分解=素数だけのかけ算にすること (例:30→2×3×5) 「約数の数を求めなさい」という問題は中学受験の 算数の問題ではよくあります。Amazonで松本 亘正, 教誓 健司の合格する算数の授業 数の性質編 (中学受験 「だから、そうなのか!素因数分解とその応用 2,3,5,7 のように、1とその数自身でしか、わりきれない数を 素数 といいます(1は素数には、ふくめません)。 整数を、素数のかけ算のかたちに分解することを 素因数分解 といいます。 たとえば12は 2×2×3 と素因数分解することができます。

中学数学3年 素因数分解の応用 約数の個数 平方数 受験の月
数の性質 中学受験 素因数 分解
数の性質 中学受験 素因数 分解- 「九九」であっても、数を「積」でイメージする事、これは「数の性質」を考える上で最も大切な操作である「素因数分解」につながっていくのです。 〇「暗算能力」を高めよう。 ② 「数に慣れる」ために、短期記憶力を高める。 階乗の素因数の個数、階乗の末尾に連続して並ぶ0の個数(ルジャンドルの公式) 10\,\kaizyou\ に含まれる素因数2の個数を求めよ$階乗の素因数の個数}}}} \\\\ 5zh 以下のように,\ $\bm {\textcolor {red} {素因数の個数を で縦に並べて,\ 横に数える}}のがポイントで



中学受験対策9 数の性質 攻略法 さんすうがく
今週の算数は素因数分解。 難解ではありませんが、簡単とも言えない問題もあります。 問題 1から50までの整数の積は6で何回割り切れますか? シンプルだけど数字の性質をちゃんと理解しないと解けません。 浜学園のテキストでは公式的に簡単に解くようになっていますが、娘に したがって素因数分解を柔軟に使えるようにしておくことが大切です。 以下のプリントもお役立ていただければと思います。 算数オンライン塾 数の性質 ===== 中学受験で子どもと普通に幸せになる方法、本日の記事は ギリギリよりは余裕のある合格の方が270を素因数分解しなさい。 ・素因数分解を利用して,次の整数の約数の個数をそれぞれ求めなさい。(32 72 126) 約数の個数と素因数分解 1から30までの整数のうち,約数が4個である整数は全部で何個ありますか。 約数の個数と素因数分解 (1)
中学受験向け約数の個数 先ほど24を素因数分解したので24の約数の個数を求めてみましょう! $$24=2^3\cdot 3$$ でしたね。 24の約数は\(2^x\cdot 3^y\)と書くことができ、\(x=0,1,2,3\)の4通り、\(y=0,1\)の2通りとなります。約数の個数は素因数分解したときの素数の種類と個数で 計算できることになります。 カードに書かれた数が奇数ですから、 素因数分解したときの素数も奇数だけです。 3×3×3×3=81 なので、 素数の個数は4個以下 とわかります。 「 × × × 」のパターンはすると、素因数分解の結果は以下のようになります。 10= 50= 100= 4000= 上記のように、 ことが分かりますね。 はい、今日も出ますよ~。 ここ 最重要ポイント ! 4000は「 」で、×2と×5が3セットなので、最後に0が3個。
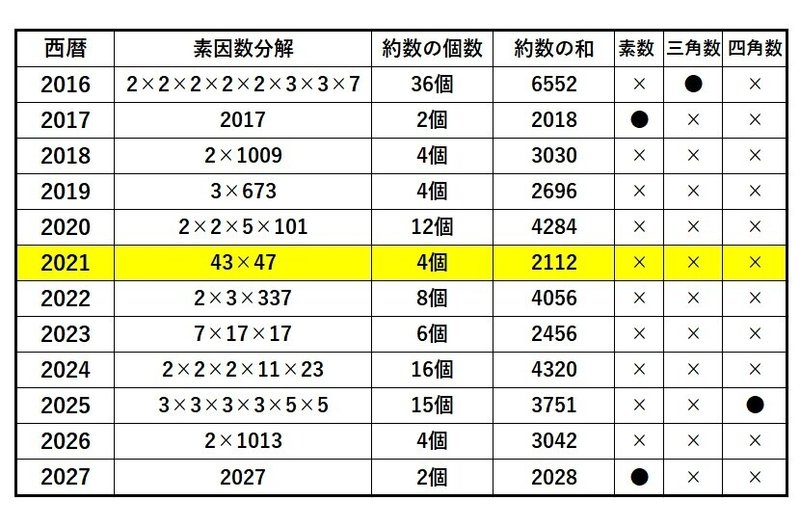
素因数分解をおこなえば、その数字が持つ性質を知ることができます。 は、=2×2×5×101と分解できました。 したがって、は2や5や101の倍数であることが分かります。 では、21を素因数分解するとどうなるでしょうか? 221を素因数分解する対象 小学5年~ 予習シリーズ該当回 5年下第7回 内容 素因数分解や,1から100までの整数の積は一の位から0が何個連続するかといった問題 数に関する問題 (1)のPDFはこちら 21年に中学受験を予定されている方はチェックしておくといいでしょう。 ① 21近辺の整数の性質について 21は素数っぽいけど素数じゃない。 21の素因数分解=43×47 というのは知らないと厳しい(その場では気付きづらい)ですね。覚えておくといい




みんなの算数オンライン 中学受験5年 数の性質2 約数と素因数分解




素因数分解のやり方のコツとは 応用問題3選も簡単に解けます 遊ぶ数学
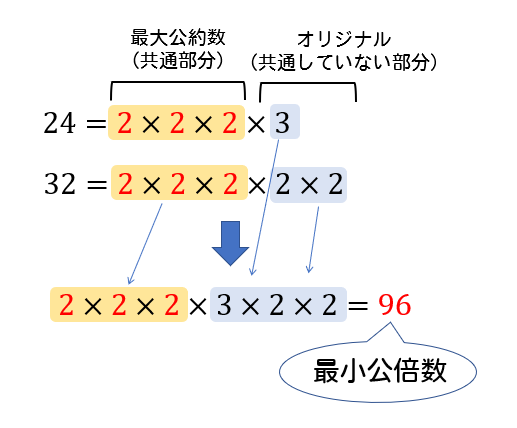
素因数分解と公倍数・公約数 がどのような関係か イメージを理解しておきましょう。 公倍数・公約数の問題を解く時は、ある2つの数の 最小公倍数と最大公約数を求めることが最も重要 です。 ですね。 ここで、素数ごとにケタを揃えて見やすくします 1.整数の性質①約数の個数の公式と素因数分解 約数として負の数(ときには0も)を含めることもありますが、考えようとしている問題によって異なります。 一応、気にはしておくべきですが、多くは定義の問題ですから、 高校数学では約数として自然数」とガツンとわかる)。アマゾンならポイント還元本が多数。松本 亘正, 教誓 健司作品ほか、お急ぎ便対象商品は当日お届けも可能。また合格する算数の授業 数の性質編 (中学受験 「だから、そう




算数テク 2で何回割り切れる 中学受験算数なら開成卒プロ家庭教師k




中学受験に出る約数の個数の求め方の分かりやすい教え方は まぜこぜ情報局
素因数分解を自在に使えるようになることが数の性質を極めるためには欠かせません。 最初は悩みますが、使いこなせるようになると受験算数ではとても強力な道具になります。 素因数分解の基本的な考え方を説明しておきます。 16を素因数分解すると 素数は自然数の世界における原子である\ 素数は特別な意味をもつ数なのである 物質であれ自然数であれ,\ その正体を探り,\ より根本を見定めることが応用上重要である 素因数分解してみることで,\ 結局その自然数が何からできているのかがわかるわけ高校受験において、整数の性質を知っておかないと解くことが困難な問題は多くあります。例えば以下の問題。皆さんは解けますか? (1) 5で割ると1あまり、6で割ると2あまる自然数のうち、0に最も近いものを求めよ。 (2) 2つの自然数の最小公倍数は100で最大公約数は5である。



算数テク 西暦問題 中学受験算数なら開成卒プロ家庭教師k




数の性質 年号を用いた問題 駒澤塾 中学受験の算数 理科
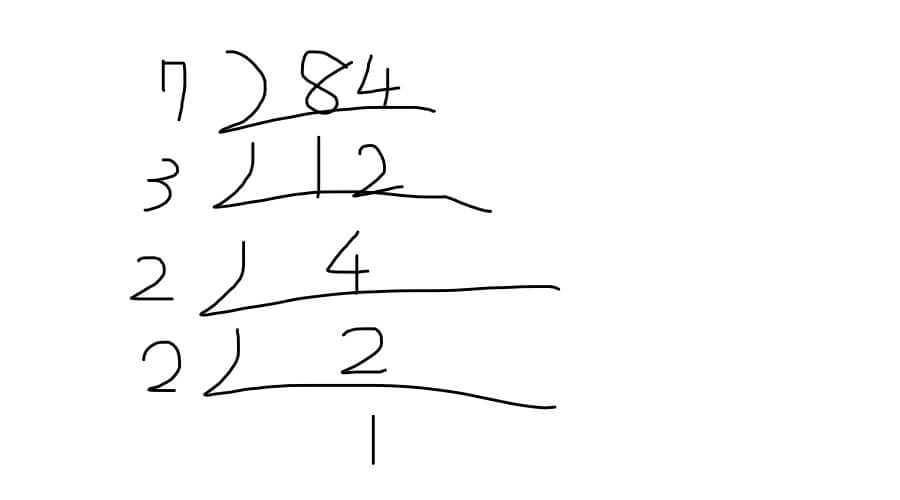
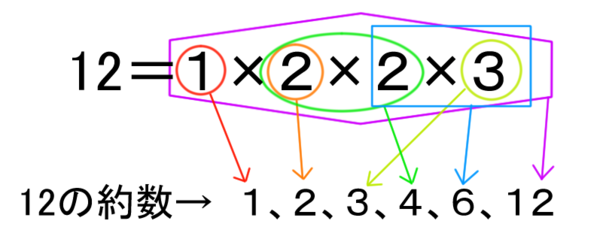
素因数分解 中学数学の素因数分解練習問題です。授業の予習、復習から定期テスト対策、受験勉強に活用してください。 次の問に答えよ。 294 に出来るだけ小さい自然数をかけて、その結果をある整数の平方にしたい。何をかければよいか。 素因数分解 「素数」とは何かがわかっていないといけません。 素数とは1より大きい自然数で、正の約数が 1 と自分自身のみであるもののことです(「自然数 」と「正」という言葉は小学生では習いませんが、無視しても大丈夫です)。 最初に約数を6個と出した「12」を「二分解法」で12を素因数分解してみます。 12→2×6→2×2×3 または 12→3×4→2×2×3 でしたね。 これを見ると、12の約数は2,3はもちろん、4や2×2、6は2×3、12は2×2×3 と皆「2」と「3」でできているのが分かります




みんなの算数オンライン 中学受験5年 数の性質2 素因数分解




約数の個数のtwitterイラスト検索結果
数字の性質を見るには、素因数分解をしてみることが大切です。 素因数分解は『正の整数を素数の積の形で表す』ことです。 例えば、12=2×2×3となります。 はどうでしょうか。 =2×2×5×101と分解することができます。 こんな計算問題が出題されそう数の性質 23 factors, prime check, fibonacci check, bell number check, binary, octal, hexadecimal representations and more 素因数分解に関しては もはや、中学受験では 必須だとは思いますが 因数分解に関しては そこまで必須とは 思いません しかし、知ってる方が 得することも あることは確かで 難関中学の受験を 目指すのであれば どんなに小さな差でも




素因数分解を使った約数の求め方 中学受験算数 Youtube




素因数分解を使った約数の求め方 中学受験算数 Youtube
スマホ向け解法集→「中学受験ー算数解き方ポータル」 参考イメージ図と解法例 極意, 算数, 中学入試, パズル, クイズ, 公約数, 数の性質, 公倍数, 約数と倍数, 素因数分解 固定リンク トラックバック素数・素因数分解 素数 約数が1と自分自身の2つしかない自然数のことを 素数 という。 次の数のうち素数はどれか。 6, 5, 1, 0 6の約数は1,2,3,6の4つあるので6は素数ではない。 5の約数は1,5の2つだけなので5は素数である。数の性質「倍数」 今回も前回に引き続き、テーマは数の性質です。 前回は「約数」について触れましたので、今回は「倍数」です。 をみていきましょう。 (問題) 2×4×6××100のように、2から100までの偶数をすべてかけた数をNとします。 (1) Nは一の位




21 の数の性質まとめ みんなの算数オンライン Note




中学数学3年 素因数分解の応用 約数の個数 平方数 受験の月
中学受験 算数プリントの主な内容 和差算 植木算 周期算 分配算 方陣算 展開図と見取図 等差数列のしくみ 円と多角形 割合の利用 百分率と歩合 消去算 代入算 円とおうぎ形 つるかめ算 平均の面積図 食塩水の問題 場合の数 ならべ方 数の性質 素因数分解とn SSとかNNという単語にピクってなる人は必読。 <数の性質>の中の1ジャンルに西暦の数字を使った問題があります。 これについて取りまとめて、今年(18年2月)の受験前に生徒に配った資料を載せます。 算数の単元としては<素因数分解><n進法><約数の個数>です。グループ指導も個別指導も、体験学習受付中! くわしくは栄光ゼミナール公式サイトへ 月 日 2 2/2 名 前 中学受験の算数 11月




数の性質 2 5 約数と素因数分解の関係 バカでもわかる 中学数学




整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ
数の性質 素因数分解を利用します。 中学入試の算数では素因数分解に関する問題が合否を分けることも少なくありません。 5年生向け 甲陽学院中学校08 数の性質 1×2×3××0 は受験算数の定番問題です。 2×4×6××0 のように連続した数ではない使用目的 毎朝今日の日付(今日で言うと)の素因数分解をしているので、答え合わせに使用しています。 ご意見・ご感想 の素数判定とか計算機なしでどうやるんだ! ? って思いました。 アンケートにご協力頂き有り難うございました次の問いの をうめなさい。 (1) 18から30までのすべての整数をかけると、一の位から0が続いて 個並ぶ。 (2) 06から18までのすべての整数をかけると4で 回割り切れる。 芝中学(18年) 男子難関校の芝中学より数の性質の問題です。 塾のテキストに載っている「何回割り切れる問題」とは一味



1




素因数分解 約数の個数の求め方を小学生にもわかりやすく教えるよ みみずく戦略室
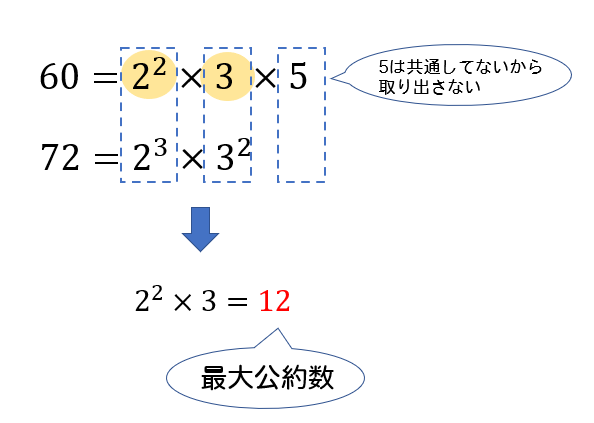
まず、54を素因数分解します。 $$54=2\times 3^3$$ そこから、それぞれの素因数を使って2乗のペアを作ります。 $$54=2\times 3^3=3^2\times 2\times 3$$ すると、2と3がペアになれずに余ってしまうことが分かりますね。 全部が2乗のペアになれば このような数を「 素数 」といいます。 素数を小さい順から挙げていくと、2、3、5、7、11、13、17、19、23、です(1は素数から除きます)。 そして、 ある整数を素数の積(かけ算)で表すこと を「 素因数分解 」といいます。 素因数分解を活用して、これらの最大公約数、最小公倍数を求めてみましょう。 (1)\(60, \ 72\) をそれぞれ素因数分解をします。 最大公約数とは、それぞれの共通する素因数をすべて取り出して掛け合わせた数。




高校数学a 自然数の分類と素因数分解の一意性 受験の月




โน ตของ 数学1 整数の性質 ช น Junior High数学 Clear



みんなの算数オンライン 中学受験 5年 数の性質2 素因数分解 例題と解説




中1 1学期 整数の性質 素因数分解 のわかりやすい教え方 教える手順 ノートのとらせ方 問題もあります ヒカリブログ ワーママhikariの目からウロコ



中学受験 約数 約数の個数 素数 最大公約数と連除法 はしご算




中学数学3年 素数と素因数分解 受験の月



数の性質 2 5 約数と素因数分解の関係 バカでもわかる 中学数学



48s96ub7b0z5f Net Seisuu Yakusuu




そうちゃ 受験図解講師for22 23 24年受験組 中学受験 を目指す 小学生 の皆さん 約数の個数 を簡単な計算で出せますか 公約数の個数 を ベン図 を書いて計算で出せますか 解き方が決まっているので 算数が苦手な人こそ 得点源 にして 摸




素因数分解 無料で使える中学学習プリント



約数の簡単な求め方を学ぼう 素因数分解についても 算数パラダイス




今さら聞けない 素因数分解の仕方と注意点




割り切る回数と素因数分解 中学受験の算数 理科ヘクトパスカル



素因数分解とは やり方やコツ 利用問題 約数など 受験辞典




算数の 暗記しておくべき数字 7選




中学受験対策9 数の性質 攻略法 さんすうがく



中学受験対策9 数の性質 攻略法 さんすうがく




中学受験 スタディサプリの算数を徹底解説します



U9j580gf8iba369ji2w Xyz P 1542




楽天ブックス 中学受験 だから そうなのか とガツンとわかる合格する算数の授業 数の性質編 松本 亘正 本




素因数分解 小5算数 偏差値45からの中学受験




算数ビレッジ Nishinomiya101 Twitter
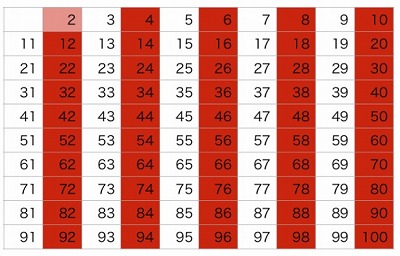



21を素因数分解するといくつ 中学受験算数に出る問題 横浜の学習塾 国大qゼミ
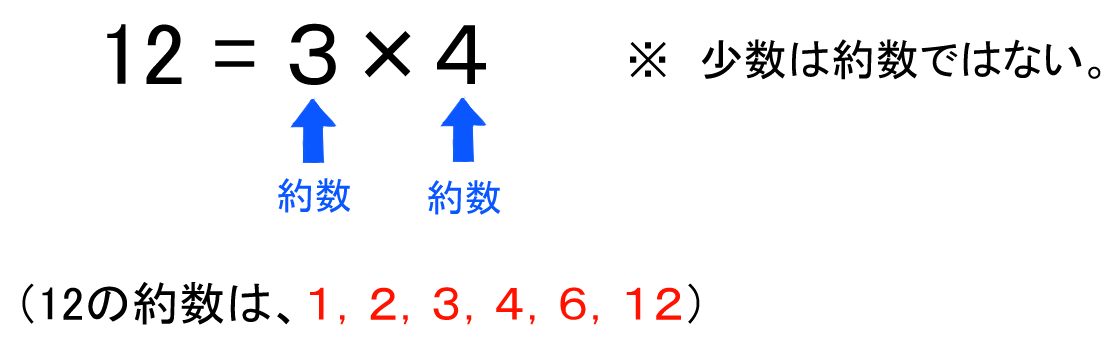



数の性質 1 約数 素数 素因数分解 バカでもわかる 中学数学




中学受験算数 J17 1 数の性質 素因数分解 偏差値50 55 基礎問題 Youtube




楽天ブックス 難関中学に合格する 数の性質トレーニング 賛数仙人の教え8 井上慶一 本



1




約数の個数の公式と平方数の性質 高校数学の美しい物語



中学受験対策9 数の性質 攻略法 さんすうがく




数a 整数の性質 まとめ 高校生 数学のノート Clear




約数の簡単な求め方を学ぼう 素因数分解についても 算数パラダイス




中学受験 公 倍数 公 約数の基礎から応用問題まで全部まとめ そうちゃ式 受験算数 新1号館 数論 特殊算
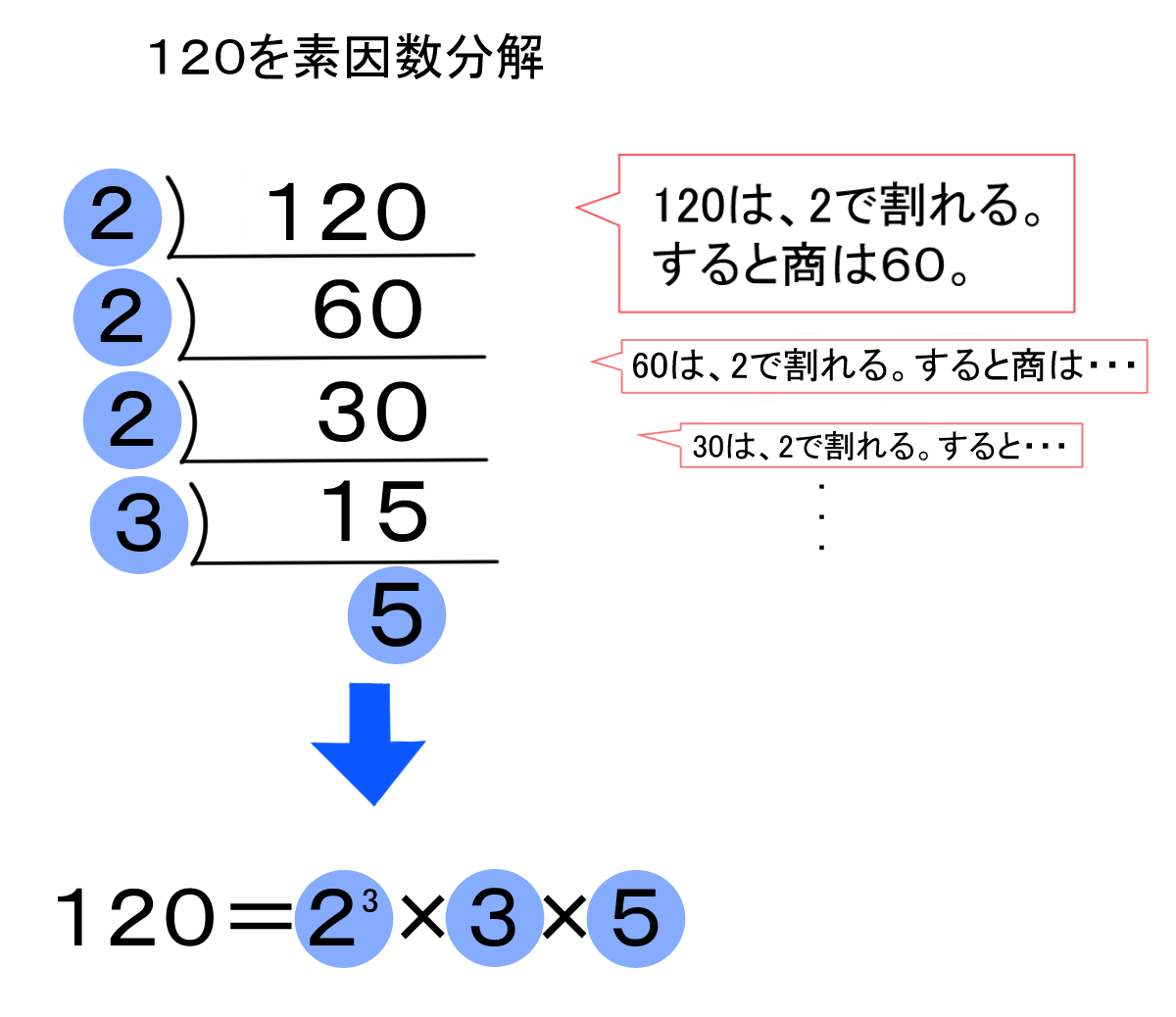



数の性質 1 約数 素数 素因数分解 バカでもわかる 中学数学




中学受験 入試問題は学校からのメッセージ ハマる問題 中学受験の下書き



9 15 素因数分解を理解するには さんすうがく パート 2
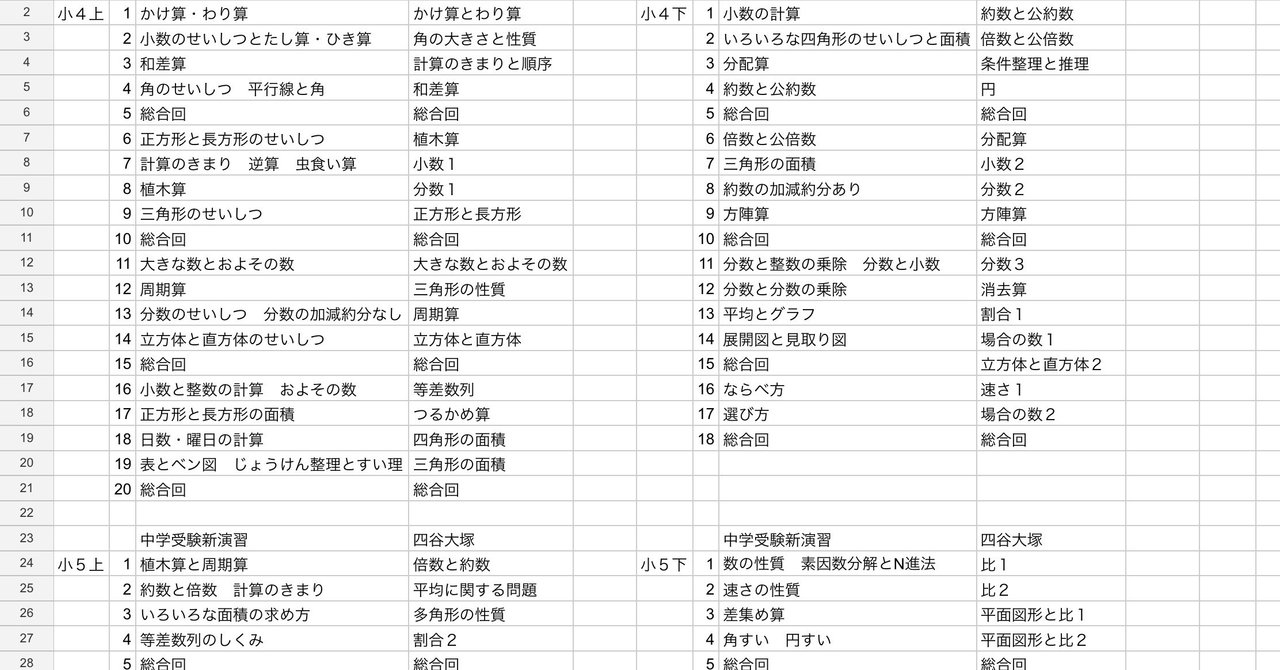



Yt予習シリーズとen中学受験新演習 井上翔一朗 オンライン中学受験算数講師 Note




算数の 暗記しておくべき数字 7選




中学受験 親子でもできるゲーム 4 5年生は素数を数えよう アベブログ




約数の個数の求め方 素因数分解すれば一発で求まる 高校生向け受験応援メディア 受験のミカタ




バカでもわかる 中学数学 数の性質 約数 倍数 素数など




公文数学の因数分解で数の性質を知る 中学受験で差が付く可能性も 地方暮らしの中学受験2024 難関中学を目指して教育格差を克服



整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ




中学受験 約数 約数の個数 素数 最大公約数と連除法 はしご




数の性質 素因数分解の利用01 保護者のための 受験 算数教室




Paypayフリマ 中学受験 新演習 算数 小5下 実力アップ問題集



3



中学受験対策9 数の性質 攻略法 さんすうがく



3




中学受験テキスト グランパは元塾長




中学受験 算数 11月 場合の数 ならべ方 数の性質 素因数分解とn進法 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ
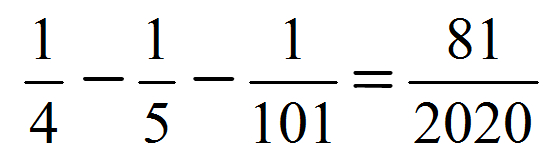



を素因数分解するといくつ 中学受験算数に出る問題 横浜の学習塾 国大qゼミ



素因数分解と約数の個数




面白い因数分解 数学天才問題 う山先生の因数分解1問目 2018年4月12日 中学受験 算数プロ家庭教師 算数合格トラの巻 エキサイト ブログ




中学受験 約数の個数の求め方は 素因数分解を活用すれば簡単です そうちゃ式 受験算数 新1号館 数論 特殊算




数の性質 約数の個数 浅野中学 15年 中学受験算数教室サンスク



素因数分解とは やり方やコツ 利用問題 約数など 受験辞典




合格する算数の授業 数の性質編 中学受験 だから そうなのか とガツンとわかる 松本 亘正 教誓 健司 本 通販 Amazon




約数の個数と約数の総和の求め方とは 公式は素因数分解で導きます 遊ぶ数学



中学受験 だから そうなのか とガツンとわかる合格する算数の授業 数の性質編 通販 セブンネットショッピング




算数の 暗記しておくべき数字 7選




21を素因数分解するといくつ 中学受験算数に出る問題 横浜の学習塾 国大qゼミ




解説動画付 予習シリーズ5年生 算数 上no14 数に関する問題のおはなし 中学受験コベツバ




素数 素因数分解 中学受験算数 Youtube




感覚算数ドリル 数の性質 入門編 前半戦 Wisardnet 中学受験算数を攻略する教材サイト




そうちゃ 受験図解講師for22 23 24年受験組 中学受験 を目指す 小学生 の皆さん 約数の個数 を簡単な計算で出せますか 公約数の個数 を ベン図 を書いて計算で出せますか 解き方が決まっているので 算数が苦手な人こそ 得点源 にして 摸



中学受験 素数 約数と すだれ算 での素因数分解のやり方 小学生 そうちゃ式 受験算数 新1号館 数論 特殊算




素因数分解応用問題 連続する数の積 中学受験算数解説 Youtube




合格する算数の授業 数の性質編 中学受験 だから そうなのか とガツンとわかる 松本 亘正 教誓 健司 本 通販 Amazon




小5受験 後期01回 数の性質 素因数分解とn進法 A 例題編 Youtube



みんなの算数オンライン 中学受験 5年 数の性質2 約数と素因数分解 例題と解説




中学受験 算数 11月 場合の数 ならべ方 数の性質 素因数分解とn進法 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ




合格する算数の授業 数の性質編 中学受験 だから そうなのか とガツンとわかる 松本 亘正 教誓 健司 本 通販 Amazon




中学受験 素数 約数と すだれ算 での素因数分解のやり方 小学生 そうちゃ式 受験算数 新1号館 数論 特殊算




上手な記憶法 知識のネット化 数の性質と場合の数 駒澤塾 中学受験の算数 理科




中学受験 算数確認チェック13 数の性質 約数 倍数 グランパは元塾長




割り切る回数と素因数分解 中学受験の算数 理科ヘクトパスカル



数の性質 倍数 前田昌宏の中学受験が楽しくなる算数塾




高校受験 私立上位校を目指す子どもが中学受験算数をやるべき理由 数学 子どものための教育支援情報サイト スタディメンター



21 の数の性質まとめ みんなの算数オンライン Note



整数の性質 最大公約数 最小公倍数の求め方と性質をイチから解説 数スタ




素因数分解と最小公倍数 最大公約数の求め方 小学生も中学生も 2つの数のすだれ算 中学受験 そうちゃ式 受験算数 新1号館 数論 特殊算



みんなの算数オンライン 中学受験5年 数の性質2 約数と素因数分解




中学受験 算数 11月 場合の数 ならべ方 数の性質 素因数分解とn進法 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ




約数の求め方 素因数分解は小学生でもできる 塾なしで中学受験をする勉強法




8 31まで おためし問題集特典つき 天才ドリル 素因数パズル 小学校3年生以上 算数 考える力を育てる 認知工学 本 通販 Amazon



中学受験 だから そうなのか とガツンとわかる合格する算数の授業 数の性質編 通販 セブンネットショッピング




算数テク 0は連続して何個並ぶ 中学受験算数なら開成卒プロ家庭教師k




数の性質 何回割り切れる 芝中学 18年 中学受験算数教室サンスク



0 件のコメント:
コメントを投稿